Téléchargez binomiale2.jar
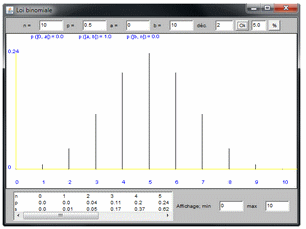
Une urne contient une proportion p de boules rouges et une proportion 1 - p de boules vertes (p compris entre 0 et 1).
On tire n boules l'une après l'autre en remettant à chaque fois la boule tirée.
On démontre alors que la probabilité de tirer k boules (k = 0, ..., n) est donnée par la formule :
![]()
Si X suit une loi binomiale de paramètre n et p alors l'espérance de X est E (X) = n p et la variance : V (X) = n p (1 - p).
Le bouton "%" permet de déterminer automatiquement l'intervalle de fluctuation (bilatéral).
Un appui sur le bouton "Ok" de la fenêtre affichage ne modifie le contenu des champs min et max.
Attention cette version utilise les "BigDecimal". Le calcul peut être très long si n est grand.